bab 3
.1. Rumus Modus
a. Rumus Modus Untuk Data Tunggal
rumus statistika modus. untuk mencari modus dari data tunggal cukup dengan mencari nilai yang banyak keluar.
contoh ada sebuah data tunggal sebagai berikut 2,3,5,7,3,4,7,8,4,6,4,5,4
dari data tunggal di atas maka modusnya adalah 4 (keluar 4 kali)
rumus statistika modus. untuk mencari modus dari data tunggal cukup dengan mencari nilai yang banyak keluar.
contoh ada sebuah data tunggal sebagai berikut 2,3,5,7,3,4,7,8,4,6,4,5,4
dari data tunggal di atas maka modusnya adalah 4 (keluar 4 kali)
b. Rumus Modus Untuk data Kelompok
keterangan
Mo = modus
c = panjang kelas (interval kelas)
Lo = batas bawah dari kelas modus,
fo = frekuensi kelas modus,
f1 = frekuensi dari kelas sebelum kelas modus,
f2 = frekuensi dari kelas setelah kelas modus
Mo = modus
c = panjang kelas (interval kelas)
Lo = batas bawah dari kelas modus,
fo = frekuensi kelas modus,
f1 = frekuensi dari kelas sebelum kelas modus,
f2 = frekuensi dari kelas setelah kelas modus
contoh sederhana
Berapa modus dari data kelompok berikut dan bagaimana cara menghitung modusnya?
Berapa modus dari data kelompok berikut dan bagaimana cara menghitung modusnya?
Batas
Kelas
|
Frekuensi
|
19,5-24,5
|
100
|
24,5-30,5
|
120
|
30,5-35,5
|
70
|
35,5-40,5
|
150
|
40,5-45,5
|
90
|
45,5-50,5
|
80
|
50,5-55,5
|
30
|
jadi
modusnya = 35,5 + 5 (80/(80+60)) = 35,5 + 5 (80/140) = 35,5 + 2,86 = 38,36
2.
Rumus Rata-rata/Rataan/Mean
a.
Rumus Rataan Data Tunggal
b. Rumus Rata-rata/Rataan/Mean Data Kelompok
fi = frekuensi untuk nilai xi yang
bersesuaian
xi = rata-rata kelas
xi = rata-rata kelas
3. Rumus Median /Nilai Tengah
a. Rumus Median Data Tunggal
b. Rumus Median Data Kelompok
L = tepi bawah dari kelas limit yang mengandung median
Me = nilai median
n = banyaknya data
Fk = frekuensi kumulatif sebelum kelas yang memuat median
fm = frekuensi kelas yang memuat median
i= panjang intreval kelas
Me = nilai median
n = banyaknya data
Fk = frekuensi kumulatif sebelum kelas yang memuat median
fm = frekuensi kelas yang memuat median
i= panjang intreval kelas
Contoh Soal
Frekuensi
|
F
Kumulatif
|
|
15-19
|
5
|
5
|
20-24
|
7
|
12
|
25-29
|
10
|
22
|
30-34
|
15
|
37
|
35-39
|
13
|
50
|
40-44
|
8
|
58
|
45-49
|
3
|
60
|
Median = 29,5 +[(30-37)/15] 5 = 27,
4.Kuartil
Istilah kuartil dalam kehidupan kita sehari-hari lebih dikenal dengan istilah kuartal.
Dalam dunia statistik, yang dimaksud dengan kuartil ialah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi ke dalam empat bagian yang sama besar, yaitu masing masing sebesar ¼ N. jadi disini akan kita jumpai tiga buah kuartil, yaitu kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3). Ketiga kuartil inilah yang membagi seluruh distribusi frekuensi dari data yang kita selidiki menjadi empat bagian yang sama besar, masing-masing sebesar ¼ N, seperti terlihat dibawah ini
Jalan pikiran serta metode yang digunakan adalah sebagaimana yang telah kita
lakukan pada saat kita menghitung median. Hanya saja, kalau median membagi
seluruh distribusi data menjadi dua bagian yang sama besar, maka kuartil
membagiseluruh distribusi data menjadi empat bagian yang sama besar.
Jika kita perhatikan pada kurva tadi, maka dapat ditarik pengertian bahwa Q2 adalah sama dengan Median(2/4 N=1/2 N).
Jika kita perhatikan pada kurva tadi, maka dapat ditarik pengertian bahwa Q2 adalah sama dengan Median(2/4 N=1/2 N).
Untuk mencari Q1,Q2 dan Q3 digunakan rumus sebagai berikut:
untuk data tunggal
Qn = 1 + ( n/4N-fkb)
fi
untuk data kelompok
Qn = 1 + (n/4N-fkb)x i
Fi
Qn = kuartil yang ke-n. karena titik kuartil ada tiga buah,
maka n dapat diisi dengan bilangan: 1,2, dan 3.
1 = lower limit ( batas bawah nyata dari skor atau interval
yang mengandung Qn).
N= Number of cases.
Fkb= frekuensi kumulatif yang terletak dibawah skor atau
interval yang mengandung Qn.
Fi= frekuensi aslinya (yaitu frekuensi dari skor atau
interval yang mengandung Qn).
i= interval class atau kelas interval.
Catatan: - istilah skor berlaku untuk data tunggal.
- istilah interval berlaku untuk data kelompok.
Berikut ini akan dikemukakan
masing-masing sebuah contoh perhitungan kuartil ke-1, ke-2, dan ke-3 untuk data
yang tunggal dan kelompok.
1). Contoh perhitungan kuartil untuk
data tunggal
Misalkan dari 60 orang siswa MAN Jurusan IPA diperoleh nilai hasil EBTA bidang
studi Fisika sebagaimana tertera pada table distribusi frekuensi berikut ini. Jika
kita ingin mencari Q1, Q2, dan Q3 (artinya data tersebut akan kita bagi dalam
empat bagian yang sama besar), maka proses perhitungannya adalah sebagai
berikut:
Table 3.11. Distribusi frekuensi nilai hasil Ebta dalam
bidang studi fisika dari 60 orang siswa MAN jurusan ipa, dan perhitungan Q1,
Q2, dan Q3.
Nilai (x)
|
F
|
Fkb
|
46
45
44
43
42
41
40
39
38
37
36
35
|
2
2
3
5
F1 (8)
10
F1 (12)
F1 (6)
5
4
2
1
|
60= N
58
56
53
48
40
30
18
12
7
3
1
|
Titik Q1= 1/4N = ¼ X 60 = 15
( terletak pada skor 39). Dengan demikian dapat kita ketahui: 1= 38,50; fi = 6;
fkb = 12
Q1 = 1 + ( n/4N-fkb) = 38,50
+(15-12)
Fi
6
= 38,50 +0,50
= 39
Titik Q2= 2/4N = 2/4 X 60 =
30 ( terletak pada skor 40). Dengan demikian dapat kita ketahui: 1= 39,50; fi =
12; fkb = 18
Q2 = 1 + ( n/4N-fkb) = 39,50
+(30-18)
Fi
12
= 39,50 +1,0
= 40,50
Titik Q3= 3/4N = 3/4 X 60 =
45 ( terletak pada skor 42). Dengan demikian dapat kita ketahui: 1= 41,50; fi =
8; fkb = 40
Q3 = 1 + ( n/4N-fkb) = 41,50
+(45-40)
Fi
8
= 41,50+ 0,625
= 42,125
2). Contoh perhitungan kuartil untuk data kelompok
Misalkan dari 80 orang siswa MAN jurusan IPS diperoleh skor hasil EBTA dalam
bidan studi tata buku sebagaimana disajikan pada tabel distribusi frekuensi
beikut ini ( lihat kolom 1 dan 2). Jika kita ingin mencari Q1, Q2, dan Q3, maka
proses perhitungannya adalah sebagai berikut:
Titik Q1= 1/4N = ¼ X 80 = 20
( terletak pada interval 35-39). Dengan demikian dapat kita ketahui: 1= 34,50;
fi = 7; fkb = 13, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi
= 34,50 +(20-13) X5
Fi
7
= 34,50 +5
= 39,50
Titik Q2= 2/4N = 2/4 X 80 =
40 ( terletak pada interval 45-49). Dengan demikian dapat kita ketahui: 1=
44,50; fi = 17; fkb = 35, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi
= 44,50 +(40-35) X5
Fi
17
= 44,50 +1.47
= 45,97
Titik Q3= 3/4N = 3/4 X 80 =
60 ( terletak pada interval 55-59). Dengan demikian dapat kita ketahui: 1=
54,50; fi = 7; fkb = 59, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi
= 54,50 +(55-59) X5
Fi
7
= 54,50 + 0,71
= 55,21
Tabel 3.12. distribusi frekuensi skor-skor hasil EBTA bidang
studi tata buku dari 80 orang siswa man jurusan ips, berikut perhitungan Q1,Q2,
dan Q3.
Nilai (x)
|
F
|
Fkb
|
70-74
65-69
60-64
55-59
50-54
45-49
40-44
35-39
30-34
25-29
20-24
|
3
5
6
7
7
17
15
7
6
5
2
|
80
77
72
66
59
52
35
20
13
7
2
|
Total
|
80= N
|
-
|
Diantara kegunaan kuartil adalah
untuk mengetahui simetris (normal) atau a simetrisnya suatu kurva. Dalam hal
ini patokan yang kita gunakan adalah sebagai berikut:
1). Jika Q3-Q2 = Q2- Q1 maka kurvanya adalah kurva normal.
2). Jika Q3-Q2 > Q2- Q1 maka kurvanya adalah kurva
miring/ berat ke kiri(juling positif).
3). Jika Q3-Q2 < Q2- Q1 maka kurvanya adalah kurva
miring/ berat ke kanan(juling negatif).
5. Desil
Desil ialah titik atau skor atau
nilai yang membagi seluruh distribusi frekuensi dari data yang kita selidiki ke
dalam 10 bagian yang sama besar, yang masing-masing sebesar 1/10 N. jadi disini
kita jumpai sebanyak 9 buah titik desil, dimana kesembilan buah titik desil itu
membagi seluruh distribusi frekuensi ke dalam 10 bagian yang sama besar.
Lambing dari desil adalah D. jadi 9 buah titik desil
dimaksud diatas adalah titik-titik: D1, D2, D3, D4, D5, D6, D7, D8, dan D9.
Perhatikanlah kurva dibawah ini:
Untuk mencari desil, digunakan rumus sebagai berikut:
Dn= 1 +(n/10N – fkb)
Fi
Untuk data kelompok:
Dn= 1+ (n/10N- fkb) xi
Fi
Dn= desil yang ke-n (disini n dapat diisi dengan bilangan:1,
2, 3, 4, 5, 6, 7, 8, atau 9.
1= lower limit( batas bawah nyata dari skor atau interval
yang mengandung desil ke-n).
N= number of cases.
Fkb= frekuensi kumulatif yang terletak dibawah skor atau
interval yang mengandung desil ke-n.
Fi= frekuensi dari skor atau interval yang mengandung desil
ke-n, atau frekuensi aslinya.
i=interval class atau kelas interval.
1). Contoh perhitungan desil untuk data tunggal
Misalkan kita ingin mencari desil ke-1, ke-5, dan ke-9 atau D1, D5, dan D9 dari
data yang tertera pada table yang telah dihitung Q1, Q2, dan Q3-nya itu.
Mencari D1:
Titik D1= 1/10N= 1/10X60= 6
(terletak pada skor 37). Dengan demikian dapat kita ketahui: 1= 5,50; fi= 4,
dan fkb= 3.
D1= 1 + (1/10N-fkb)
---D1=36,50 (6-3)
Fi
4
= 36,25
Mencari D5:
Titik D5= 5/10N= 5/10X60= 30
(terletak pada skor 40). Dengan demikian dapat kita ketahui: 1= 39,50; fi= 12,
dan fkb= 18.
D1= 1 + (5/10N-fkb)
---D1=39,50 (30-18)
Fi
12
= 40,50
Mencari D9:
Titik D9= 9/10N= 9/10X60= 54
(terletak pada skor 44). Dengan demikian dapat kita ketahui: 1= 43,50; fi= 3,
dan fkb= 53.
D1= 1 + (9/10N-fkb) ---D1=
43,50 (54-53)
Fi
3
= 43,17
Tabel 3.13. Perhitungan desil ke-1, desil ke-5 dan desil
ke-9 dari data yang tertera pada table (diatas) kuartil.
Nilai (x)
|
F
|
Fkb
|
46
45
44
43
42
41
40
39
38
37
36
35
|
2
2
3
5
8
10
12
6
5
4
2
1
|
60= N
58
56
53
48
40
30
18
12
7
3
1
|
2). Contoh perhitungan desil untuk data kelompok
Misalkan kita ingin mencari D3 dan D7 dari data yang tercantum pada table 3.12,
proses perhitungannya adalah sebagai berikut:
Table 3.14. Perhitungan desil ke-3 dan desil ke-7 dari data
yang tertera pada table 3.12.
Nilai (x)
|
F
|
Fkb
|
70-74
65-69
60-64
55-59
50-54
45-49
40-44
35-39
30-34
25-29
20-24
|
3
5
6
7
7
17
15
7
6
5
2
|
80
77
72
66
59
52
35
20
13
7
2
|
Total
|
80= N
|
-
|
Mencari D3:
Titik D3= 3/10N= 3/10X80= 24
(terletak pada interval 40-44). Dengan demikian dapat kita ketahui: 1= 39,50;
fi= 15, dan fkb= 20.
D3= 1 + (3/10N-fkb) xi=39,50
(24-20) x 5
Fi
15
= 39,50+ 20= 39,50 + 1,33= 40,83
15
Mencari D7:
Titik D7= 7/10N= 7/10X80= 56
(terletak pada interval 50-54). Dengan demikian dapat kita ketahui: 1= 49,50;
fi= 7, dan fkb= 52.
D7= 1 + (7/10N-fkb) xi=49,50
(50-54) x 5
Fi
7
= 49,50+ 20= 49,50 + 2,86= 40,83
7
Diantara kegunaan desil ialah untuk menggolongkan-golongkan suatu distribusi
data ke dalam sepuluh bagian yang sama besar, kemudian menempatkan
subjek-subjek penelitian ke dalam sepuluh golongan tersebut.
6. Persentil
Persentil yang biasa dilambangkan P,
adalah titik atau nilai yang membagi suatu distribusi data menjadi seratus
bagian yang sama besar. Karena itu persentil sering disebut ukuran
perseratusan.
Titik yang membagi distribusi
data ke dalam seratus bagian yang sama besar itu ialah titik-titik: P1, P2, P3,
P4, P5, P6, … dan seterusnya, sampai dengan P99. jadi disini kita dapati
sebanyak 99 titik persentil yang membagi seluruh distribusi data ke dalam
seratus bagian yang sama besar, masing-masing sebesar 1/ 100N atau 1%, seperti
terlihat pada kurva dibawah ini:
Untuk mencari persentil digunakan rumus sebagai berikut:
Untuk data tunggal:
Pn= 1 +(n/10N – fkb)
Fi
Untuk data kelompok:
Pn= 1+ (n/10N- fkb) xi
Fi
Pn= persentil yang ke-n (disini n dapat diisi dengan
bilangan-bilangan:1, 2, 3, 4, 5, dan seterusnya sampai dengan 99.
1= lower limit( batas bawah nyata dari skor atau interval
yang mengandung persentil ke-n).
N= number of cases.
Fkb= frekuensi kumulatif yang terletak dibawah skor atau
interval yang mengandung persentil ke-n.
Fi= frekuensi dari skor atau interval yang mengandung
persentil ke-n, atau frekuensi aslinya.
i= interval class atau kelas interval.
Tabel. 3.15. Perhitungan persentil ke-5, persentil ke-20 dan
persentil ke-75 dari data yang tertera pada tabel 3.13.
Nilai (x)
|
F
|
Fkb
|
70-74
65-69
60-64
55-59
50-54
45-49
40-44
35-39
30-34
25-29
20-24
|
3
5
6
7
7
17
15
7
6
5
2
|
80
77
72
66
59
52
35
20
13
7
2
|
Total
|
80= N
|
-
|
1). Contoh perhitungan desil untuk data tunggal
Misalkan kita ingin mencari persentil ke-5 (P5), persentil ke-20 (P20), dan
ke-75 (P75),dari data yang disajikan pada tabel 3.13 yang telah dihitung
desilnya itu. Cara menghitungnya adalah sebagai berikut:
Mencari persentil ke-5 (P5):
Titik P5= 5/10N= 5/10X60= 3
(terletak pada skor 36). Dengan demikian dapat kita ketahui: 1= 35,50; fi= 2,
dan fkb= 1.
P5= 1 + (5/10N-fkb) =36,50 +(3-1)
Fi
2
= 36,50
Mencari persentil ke-75
(P75):
Titik P75= 75/10N= 75/10X60= 45
(terletak pada skor 42). Dengan demikian dapat kita ketahui: 1= 41,50; fi= 8,
dan fkb= 40
P75= 1 + (75/10N-fkb) =41,50
+(45-40)
Fi
8
= 42,125
2). Cara mencari persentil untuk data kelompok
Misalkan kembali ingin kita cari P35 dan P95 dari data yang disajikan pada
tabel 3.14.
Mencari persentil ke-35
(P35):
Titik P35= 35/100N= 35/100X80= 28
(terletak pada interval 40-44). Dengan demikian dapat kita ketahui: 1= 39,50;
fi= 15, dan fkb= 20, i=5
P35= 1 + (35/100N-fkb) Xi
=39,50 +(45-40) X 5
Fi
8
= 39,50+2,67
= 42,17
Mencari persentil ke-95
(P95):
Titik P95= 95/100N= 95/100X80= 76
(terletak pada interval 65-69). Dengan demikian dapat kita ketahui: 1= 64,50;
fi= 5, dan fkb= 72, i=5
P95= 1 + (95/100N-fkb) Xi
=64,50 +(65-69) X 5
Fi
5
= 64,50+4
= 68,50
Tabel 3.16. Perhitungan persentil ke-35 dan persentil ke-95
dari data yang tertera pada tabel 3.14.
Nilai (x)
|
F
|
Fkb
|
70-74
65-69
60-64
55-59
50-54
45-49
40-44
35-39
30-34
25-29
20-24
|
3
5
6
7
7
17
15
7
6
5
2
|
80
77
72
66
59
52
35
20
13
7
2
|
Total
|
80= N
|
-
|
Kegunaan persentil dalam dunia pendidikan adalah:
- Untuk mengubah rawa score (raw data) menjadi standard score (nilai standar).
Dalam dunia pendidikan, salah satu standard score yang
sering digunakan adalah eleven points scale ( skala sebelas nilai) atau dikenal
pula dengan nama standard of eleven (nilai standard sebelas) yang lazim
disingkat dengan stanel.
Pengubahan dari raw score menjadi
stanel itu dilakukan dengan jalan menghitung: P1- P3- P8- P21- P39- P61- P79-
P92- P97- dan P99.
Jika data yang kita hadapi berbentuk
kurva normal (ingat: norma atau standar selalu didasarkan pada kurva normal
itu), maka dengan 10 titik persentil tersebut diatas akan diperoleh nilai-nilai
standar sebanyak 11 buah, yaitu nilai-nilai 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, dan
10.
- Persentil dapat digunakan untuk menentukan kedudukan seorang anak didik, yaitu: pada persentil keberapakah anak didik itu memperoleh kedudukan ditengah-tengah kelompoknya.
- Persentil juga dapat digunakan sebagai alat untuk menetapkan nilai batas lulus pada tes atau seleksi.
Misalkan sejumlah 80 orang individu seperti yang tertera
pada tabel 3.16. itu hanya akan diluluskan 4 orang saja (=4/ 80 X 100%= 5%) dan
yang tidak akan diluluskan adalah 76 orang (= 76X80 X 100%=95%), hal ini
berarti bahwa P95 adalah batas nilai kelulusan. Mereka yang nilai-nilainya
berada pada P95 kebawah, dinyatakan tidak lulus, sedangkan diatas P95
dinyatakan lulus. Dalam perhitungan diatas telah kita peroleh P95= 68,50;
berarti yang dapat diluluskan adalah mereka yang nilainya diatas 68,50 yaitu
nilai 69 ke atas.
Sumber :
Sudjana. (1991). In Statistika. Bandung: Tarsito.bab 5
MOMEN, KEMIRINGAN, DAN KURTOSIS
Skewness
and Kurtosis
Rata-rata dan ukuran penyebaran
dapat menggambarkan distribusi data tetapi tidak cukup untuk menggambarkan sifat
distribusi. Untuk dapat menggambarkan karakteristik dari suatu distribusi
data, kita menggunakan konsep-konsep lain yang dikenal sebagai kemiringan (skewness)
dan keruncingan (kurtosis).
Skewness
Kemiringan (skewness) berarti
ketidaksimetrisan. Sebuah distribusi dikatakan simetris apabila nilai-nilainya
tersebar merata disekitar nilai rata-ratanya. Sebagai contoh, distribusi data
berikut simetris terhadap nilai rata-ratanya, 3.
x
|
1
|
2
|
3
|
4
|
5
|
frek (f)
|
5
|
9
|
12
|
9
|
5
|
Pada contoh gambar berikut,
distribusi data tidak simetris. Gambar pertama miring (menjulur) ke arah kiri
dan gambar ke-2 miring ke arah kanan.
Pada distribusi data yang simetris,
mean, median dan modus bernilai sama.
Beberapa langkah-langkah perhitungan
digunakan untuk menyatakan arah dan tingkat kemiringan dari sebaran data.
Langkah-langkah tersebut diperkenalkan oleh Pearson.
Koefisien kemiringan(Coefficient of
Skewness):
Interpretasi: Untuk distribusi data yang simetris, Sk = 0. Apabila
distribusi data menjulur ke kiri (negatively skewed), Sk bernilai
negatif, dan apabila menjulur ke kanan (positively skewed),
SK bernilai positif. Kisaran untuk SK antara -3 dan 3.
Ukuran kemiringan yang lain adalah
koefisien β1 (baca 'beta-satu'):
dimana:
Interpretasi:
Distribusi dikatakan simetris
apabila nilai b1 = 0. Skewness positif atau negatif tergantung pada
nilai b1 apakah bernilai positif atau negatif.
Ukuran
Skewness yang sering digunakan:
Skewness Populasi:
Skewness Sampel:
Source: D. N. Joanes and C. A. Gill.
"Comparing Measures of Sample Skewness and Kurtosis". The
Statistician 47(1):183–189.
atau formula berikut (MS Excel):
s = standar deviasi
NB: kedua formula di atas
menghasilkan nilai skewness yang sama
Interpretasi:
Distribusi dikatakan simetris
apabila nilai g1 = 0. Skewness positif atau negatif tergantung pada
nilai g1 apakah bernilai positif atau negatif.
Menurut Bulmer, M. G., Principles of
Statistics (Dover, 1979):
- highly skewed: jika skewness kurang dari −1 atau lebih dari +1
- moderately skewed: jika skewness antara −1 dan −½ atau antara +½ dan +1.
- approximately symmetric: jika skewness is berada di antara −½ dan +½.
Kurtosis
Kurtosis merupakan ukuran untuk
mengukur keruncingan distribusi data.
Distribusi pada gambar di atas
semuanya simetris terhadap nilai rata-ratanya. Namun bentuk ketiganya tidak
sama. Kurva berwarna biru dikenal sebagai mesokurtik (kurva normal),
kurva berwarna merah dikenal sebagai leptokurtik (kurva runcing) dan
kurva berwarna hijau dikenal sebagai platikurtik (kurva datar).
Kurtosis dihitung dengan menggunakan
koefisien Pearson, β2 (baca 'beta - dua').
dimana:
Ukuran
Kurtosis yang sering digunakan:
Kurtosis Populasi:
Kurtosis:
Excess Kurtosis:
Kurtosis Sampel:
atau formula berikut (MS Excel):
s = standar deviasi
NB: Excel menggunakan nilai Excess
Kurtosis. Hasil perhitungan dari kedua formula di atas, menghasilkan nilai yang
sama
Interpretasi:
Distribusi dikatakan:
- Mesokurtik (Normal) jika b2 = 3
- Leptokurtik jika b2 > 3
- platikurtik jika b2 < 3
Analisis Korelasi Product Moment dalam Statistika
Analisis korelasi merupakan salah
satu teknik statistik yang digunakan untuk menganalisis hubungan
antara dua variabel atau lebih yang bersifat kuantitatif. Salah satu
dari analisis korelasi tersebut adalah analisis korelasi product
moment (Pearson). Variabel yang digunakan disini terbagi dua yaitu
variabel bebas (x) dengan variabel terikat (y), dengan ketentuan data
memiliki syarat-syarat tertentu.
Korelasi Pearson Product Moment (r) dapat diformulasikan sbb:

dengan ketentuan −1 ≤ r ≤ r . Dan interpretasi koefisien korelasi nilai r ini dapat dirangkum dalam tabel berikut:

Langkah-langkah yang diperlukan untuk uji korelasi Pearson Product Moment adalah sebagai berikut :
Korelasi Pearson Product Moment (r) dapat diformulasikan sbb:

dengan ketentuan −1 ≤ r ≤ r . Dan interpretasi koefisien korelasi nilai r ini dapat dirangkum dalam tabel berikut:

Langkah-langkah yang diperlukan untuk uji korelasi Pearson Product Moment adalah sebagai berikut :
- Rumuskan hipotesis Ha dan Ho dalam bentuk kalimat.
- Rumuskan hipotesis Ha dan Ho dalam bentuk statistik.
- Buat tabel pembantu.
- Tentukan r
- Tentukan nilai KP
- Lakukan uji signifikansi.
- Tentukan α , dengan derajat bebas db = n − 2 .
- Tentukan konklusi
SUMBER :
http://navy.blogspot.com/2013/10/analisis-korelasi-product-moment-dalam.html
http://navy.blogspot.com/2013/10/analisis-korelasi-product-moment-dalam.html
Luas
dibawah kurva satu.
Daftar
distribusi normal berisikan nilai-nilai F untuk peluang 0,01 dan 0,05 dengan
derajat
kekebasan v1 dan v2. Peluang ini sama dengan luas daerah ujung kanan yang
diarsir,
sedangkan derajat kekebasan pembilang (v1 ) ada pada baris paling atas dan
derajat
kebebasan penyebut (v2) pada kolom paling kiri.
Notasi lengkap untuk
nilai-nilai F dari daftar distribusi F dengan peluang p dan dk = (v1,v2) adalah Fp(v1,v2). Demikianlah untuk contoh kita didapat :
F0.05(24,8) = 3.12 dan F0,01(24,8 )= 5.28.
Meskipun
daftar yang diberikan hanya untuk peluang p = 0.05 dan p = 0.01, tetapi
sebenarnya masih bisa didapat nilai-nilai F dengan peluang 0,99 dan 0,95. Untuk
ini digunakan hubungan :
Dalam rumus diatas perhatikan
antara p dan (1- p) dan pertukaran antara derajat kebebasan (v1, v2 )
menjadi (v2, v1).
sumber;
http://www.riny.blogspot.html
http://wikipedia_statistika.html
 .
. .
.
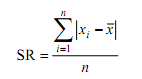
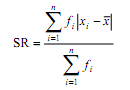
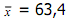
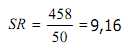
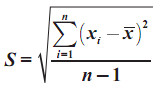
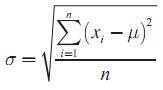
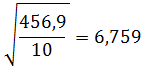
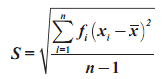
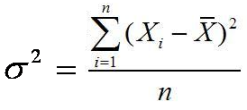
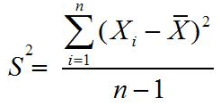
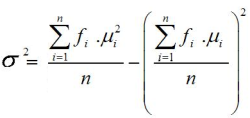
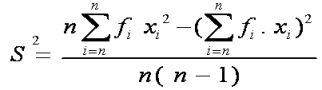
















keren!!!
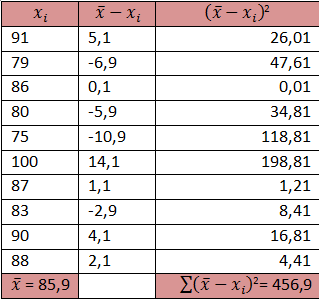
BalasHapusMaksud dari simpangan baku populasi
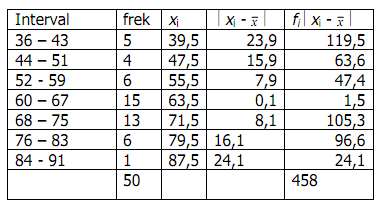
BalasHapus-^x-xi dibawahnya 5,1 bawah lagi -6,9 bawah lagi 0,1 bawah lagi -5,9 bawah lagi -10,9 itu apaan ?dapat dari mana
nilai ujian statistik mahasiswa prodi ekonomi kelas A12 dan kelas A13
BalasHapusA12 : 80 83 82 70 74 60 90 84 93 86 85 74 75 70 76 90 87 76 68 80
A13 : 87 86 87 83 90 94 65 68 69 90 93 84 85 97 60 65 74 73 76 78
Buktikan hipotesis bahwa tidak terdapat perbedaan yang signifikan antara nilai ujian statistik mahasiswa prodi ekonomi
Jumlah kredit
BalasHapusJutaan rupiah. Frekuensi
10-19. 1
20-29. 3
30-39. 8
40-49. 15
50-59. 32
60-69. 20
70-79. 14
80-89. 6
90-99. 1
Berdasarkan data trsebut di atas maka
1 hitunglah koefesien kemiringannya dengan menggunakan nilai kuartil
2. Tentukan model distribusi dari data d atas di tinjau dari segi kemiringannya
3. Hitunglah koefisien keruncingannya ( kurtosis)
4. Tentukan model distribusi dari data di atas di tinjau dari segi keruncingannya.
genesis noir switch - LCbet.com fun88 soikeotot fun88 soikeotot 카지노 카지노 dafabet dafabet 8209Best Live Football Prediction Site for Free
BalasHapusThe Game: Top 10 slots and casinos to play in 2021 - JTM Hub
BalasHapusTop 천안 출장안마 10 slots 문경 출장안마 and casinos to play 동해 출장안마 in 2021 · 충주 출장마사지 Wolf Gold · Rainbow Riches · Red Tiger · Supernova · Sweet Bonanza · Wild 계룡 출장마사지 Gold.